Production function

A production function shows how a firm turns inputs - like labor, capital, and materials - into output. It helps you understand how different combinations of inputs affect the amount a business can produce, and why adding more of one input doesn’t always increase output at the same rate.

How the production function works

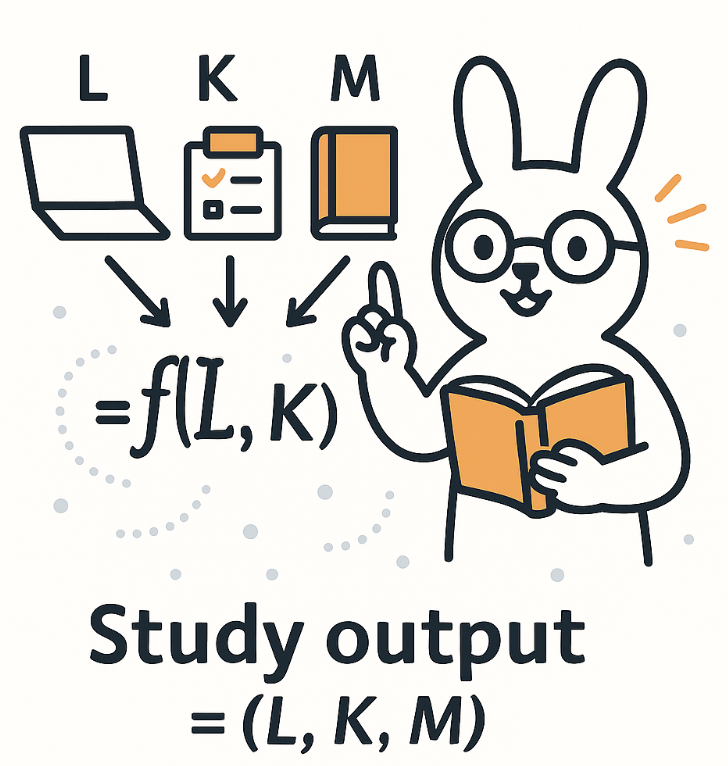
A production function shows how different inputs combine to create output. It’s written as Q = f(L, K, M), where L is labor (often measured in hours), K is capital (like machines or tools), and M is materials. By changing one or more of these inputs, you can see how the level of output responds.

Firms use this relationship to test different input combinations - for example, what happens to output if they add more labor hours, upgrade equipment, or use more materials. The production function makes these connections clear by mapping each input mix to a specific level of output.

‍

How Alice could help

Production functions involve inputs, outputs, and shifting productivity - which can get confusing when you’re juggling graphs and concepts like marginal product. Alice turns your material into clear notes, summaries, and quizzes, helping you see how output changes as inputs increase and where diminishing returns start to appear. You spend less time stuck on theory and more time understanding the patterns.

‍

Try Alice for free

Example o a production function in real life

Imagine that you’re preparing for exams and want to predict how much revision you can finish in a week. Your “output” is the amount of study material you cover, and your inputs are things like L (hours you study), K (your laptop, notes, and digital tools), and M (practice tests, textbooks, or problem sets).

Your personal production function might look like:

Study output = f(L, K, M)

If you increase your study hours (L), upgrade your tools (K) with something like Alice, or add new practice material (M), your study output changes in predictable ways.

This is exactly what a production function does - it shows how different combinations of inputs lead to different levels of output, even in your own study routine.

‍

Why production function matters

Real-world use

Production functions help firms understand how labor, capital, and resources contribute to output, guiding decisions about hiring, investment, and equipment.

‍

Relevance

They show how productivity changes as more inputs are added, making them essential for understanding costs, efficiency, and the logic behind diminishing returns.

‍

Impact

By revealing how inputs translate into output, production functions help businesses optimize their operations and avoid wasting resources on inputs that add little extra value.

‍

Still have questions?

What are the inputs in a production function?

Most production functions include labor (L), capital (K), and materials (M). These are the inputs a firm combines to produce output, and the function shows how each one contributes to total production.

What are the main types of production functions?

Common forms include the Cobb-Douglas, Leontief, and linear production functions. Each one represents a different relationship between inputs and output depending on how easily inputs can substitute for one another.

What are the three phases of a production function?

The three phases are increasing returns (output rises quickly), diminishing returns (output rises but more slowly), and negative returns (adding more input reduces output). These phases show how productivity changes as inputs increase.

How do firms use production functions in real life?

Firms use them to plan hiring, choose equipment, forecast output, and test different input combinations. It helps them find the most efficient way to produce goods or services at the lowest possible cost.

Try Alice, make your study inputs more productive

A production function shows how inputs turn into output - and studying works the same way. Alice helps you get more out of every study hour by turning your material into clear notes, summaries, and quizzes.